Информация и вероятность
В 2009 году репетиционный ЕГЭ по информатике готовил и проводил Федеральный центр тестирования. Неожиданно для многих в этом тесте появились задачи на определение количества информации в случае неравновероятных событий. Скорее всего, такие задачи не встретятся на реальном экзамене, по крайней мере, в ближайшее время. Однако, не исключено, что «вброс» заданий нового типа был «пробным камнем».
Судя по тем письмам, которые я получаю, существует страшная путаница в этом вопросе, даже среди преподавателей ВУЗов. Далее приведены распространенные заблуждения и сделана попытка прояснить ситуацию.
Задача. В корзине 32 клубка шерсти, из них 4 клубка красного цвета. Какое количество информации несет сообщение «Вытащили клубок красной шерсти»?
Заблуждение 1. Количество информации равно 1 бит, потому что эта информация равносильно ответу на вопрос: «Верно ли, что вытащили клубок красной шерсти (да/нет)»? Как мы хорошо знаем, ответ на вопрос «да или нет» несет 1 бит информации.
В самом деле, количество информации равно 1 бит только в том случае, если два события равновероятны. В данном случае это не так, поскольку вероятность вытащить красный клубок равна 4/32=1/8, а вероятность вытащить некрасный клубок равна 28/32=7/8. Поэтому количество информации нужно вычислять с учетом вероятности как собственную информацию или количественную меру Шеннона: если произошло событие, имеющее вероятность p, то информация в сообщении об этом событии равна
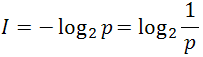 | (1) |
Заблуждение 2. Количество информации в случае неравновероятных событий вычисляется по формуле Шеннона:
| (2) |
где N — число возможных событий, а pi (i=1,...,N) — вероятности отдельных событий.
В самом деле, по этой формуле считается информационная энтропия (неопределенность), а не информация, полученная в сообщении о конкретном событии. Сравнивая формулы (1) и (2), несложно понять, что энтропия H — это средняя информация, математическое ожидание от частных значений, вычисляемых по формуле (1) для каждого события.
Для тех, кто сомневается (и правильно делает!) укажем авторитетный источник: книгу «Теория информации» выдающегося математика XX века Р.Л. Стратоновича (М.: Советское радио, 1975, с. 13-14).
Ярлыки: information, probability, Shannon


Комментарии: 1:
Спасибо, Константин Юрьевич! Запись Ваша от 6.01. Значит и на каникулах работали. Спасибо за все, что Вы делаете! Всех благ Вам в наступившем году!
Отправить комментарий
<< Главная страница